Hello, and welcome.
My intention here is to provide a way to define the term
"diffraction limited"
By John Sherman
Mel Bartels said:
"The term 'diffraction limited' has so many meanings that it is meaningless."
http://www.bbastrodesigns.com/ratemirrors.html
And how right he is.
Why should we put up
with lots of different meanings? All it does is confuse people.
Like,
us, for example. Since there is a good definition for "diffraction
pattern" and for "limited", I think it should be easy to come up with a
definition for "diffraction limited". Since this term is so frequently
bandied about, it behooves us to determine a standard definition. Diffraction
spreads out the light from a star into a pattern, and that limits the quality of
the view through a telescope (or other lens). It is commonly defined that if
a Root Mean Square deviation of lots of measurements of your wavefront equals
0.07 wave or less, then your system is diffraction limited. A Strehl ratio of
80% or better is about equivalent. It is obvious that if 20% extra light is
robbed from Airy's disc by aberrations and fed into his diffraction rings (which
is the definition of Strehl ratio 80%), then the system is NOT diffraction
limited, and the difference is DECIDEDLY prejudicial to the human eye (in spite
of the atmosphere we are forced to look through) (roughly requoting Lord
Rayleigh, here). It seems very curious to me...
I'll start with this:
A limit is a barrier you cannot go beyond. Diffraction limited means diffraction is that barrier. You have reached the limit, so there is no way you can go beyond where you are. If your telescope does not produce a perfect diffraction pattern, it is not "diffraction limited". In a perfect telescope 84% of the light from a star goes into the central diffraction disc and 16% goes into the diffraction rings. That gives a Strehl ratio of 100%. That telescope is diffraction-limited, meaning the image is limited by diffraction only. If your telescope only puts nine-tenths of the allowable 84% of the total light into the disc, then your telescope has a Strehl ratio of 90%. If your telescope has any obstructions in the light path, then those obstructions function as an aberration by lowering the maximum amount of light in the diffraction disc. In such telescopes the calculation of the Strehl ratio usually begins from this lower number. Either way, diffraction limited means that you have a Strehl ratio of 100%.
If you can go beyond where you are, then you are not at the limit.
If the system can deliver a better image, then it is not limited by diffraction only. It is "diffraction AND aberration limited". An optical system limited only by diffraction will not show any other aberrations. If it does show other aberrations, the image will be degraded, and therefore it is limited by aberrations and by diffraction. An optical system providing an image which is called "diffraction limited", will not have any other aberrations evident. So what we want to do here is to have a telescope, which we can examine with a star, and the only limitation we see is diffraction (other than seeing).
So what can we see?
So, you have a diffraction limited telescope, have you? Focus a star in excellent seeing at high power and you will see a diffraction pattern. There is an Airy diffraction pattern, consisting of a disc with a few rings around it. Move the focus in and out and you see a bulls eye pattern on each side of focus, they should be identical. If they are not identical, then the in-focus image will be degraded below the limitation imposed by diffraction. Any defects visible out of focus are also visible in focus, although they are more subtle when in focus. If you have any geometrical aberrations (spherical or chromatic aberrations, astigmatism, collimation or fabrication errors, etc), these problems are in ADDITION to the diffraction pattern. One definition is to say that, "Because the starlight entering your telescope passed an aperture, some of it is deflected into a diffraction pattern. That pattern contains the Airy disc, and there is no possible way to get rid of it. If the geometrical aberrations are minimized to the point where they spread out the light from the star into a disc no larger than the Airy disc, then the system is diffraction limited. That is because the aberrations are hidden behind the disc, which you always have to look at, anyway."
Is that really the limit?
Nope! It is evident that we want to concentrate as much light as possible into the very center of the Airy disc. If we allow aberrations to fill the entire Airy disc with light, it will appear uniformly illuminated. But an Airy disc should show a very high intensity at the very center, and then rapidly dim towards the edge. If you fill the edge of the disc with light from other problems, then it's appearance will be changed. Your telescope will not be diffraction limited.
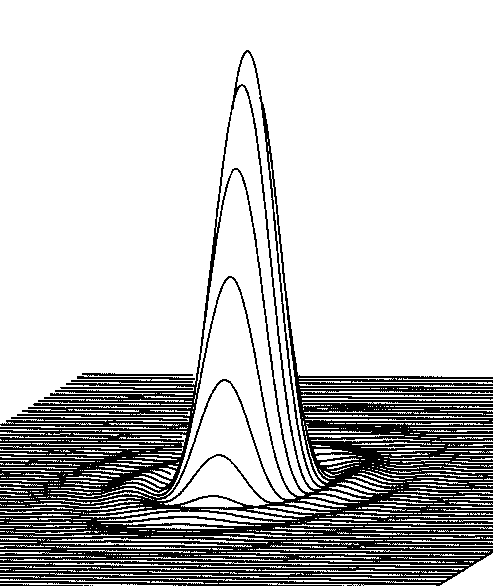
This is a diagram of
a perfect diffraction pattern. It is taken from:
Practical Computer-Aided
Lens Design, by GH Smith, pg 135.
An excellent book. When you see a star in
your telescope you are seeing this pattern from the top.
On the left side below is a representation of the above diagram. On the right is shown a representation of an Airy disc filled with light from aberrations. The disc is shorter and it is now smaller in diameter. It contains less light as there is now more light in the rings. And, in spite of having a smaller diameter at the bottom, it has a fatter overall profile due to the aberrations in the scope.
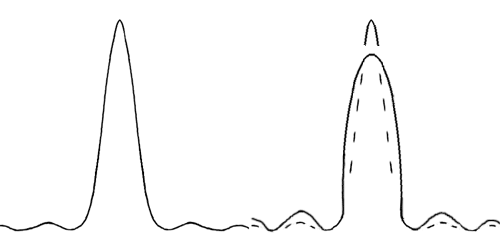
When viewing the
pattern on the right, one might expect to see an Airy disc which is more evenly
illuminated. There would be a sharp rise in brightness from the first dark ring
at the edge of the disc. There may be a vague brighter area near the center.
When viewing the pattern on the left, however, we can see the outside edge of
the Airy disc to only be a little brighter than the first diffraction ring. The
light is concentrated towards the center of the disc, and has a bright starlike
point in the center.
Of course, if we cannot actually SEE the difference
between the perfect pattern above, compared to one where the Airy disc is full
of light, then they would both be diffraction limited for our visual purposes.
But if the difference is visible, it means the pattern on the right is not
diffraction limited by any honest definition. It all depends on what we can
actually see, through our own telescopes, in our own atmosphere. If we can see a
better view than the one on the right, then that view is not the limit. Why
should we settle for optics that make a star look like a disc, when we could
have optics that make a star look like a star which is embedded in a faint
disc?
So, what can we see??
In order to see the
difference in these two images, we need an experienced observer looking through
excellent seeing with a very high quality telescope. While it would be nice to
have scientific verification, complete with photographs, all we need is one
witness whom we do not doubt. In a post to the ATM List, dated
3/12/1, Mel Bartels said:
"Stars too at very
high magnifications are a pleasant surprise. On nights of excellent seeing, the
airy disk is not seen, rather, a small pinpoint of light representing the
brightest portion of the airy disk is visible. This makes globular clusters in
large scopes still appear as a tremendous city of pinpoint lights."
If your wavefront does not produce a perfect diffraction pattern, then it is not diffraction limited.
Thank you, Mel, for showing it to us.
We now have meaning.
And
I have heard that there is indeed photographic proof floating around, but I
don't know where it is. Supposedly someone took a series of photographs of a
star at very high magnification through a series of gradually darker neutral
density filters, and found that the Airy disc does indeed get smaller with the
darker filters. Using shorter and shorter exposures should do the same thing.
With such an arrangement it might be possible to measure the brightness curve of
the disc in different telescopes of varying aberrations. I welcome any and all
comments and
testimonials! It would be nice if someone else could verify Mel's
observation. I only have one telescope which might be sharp enough to show the
star in the Airy pattern. I will be looking for some good
seeing....
